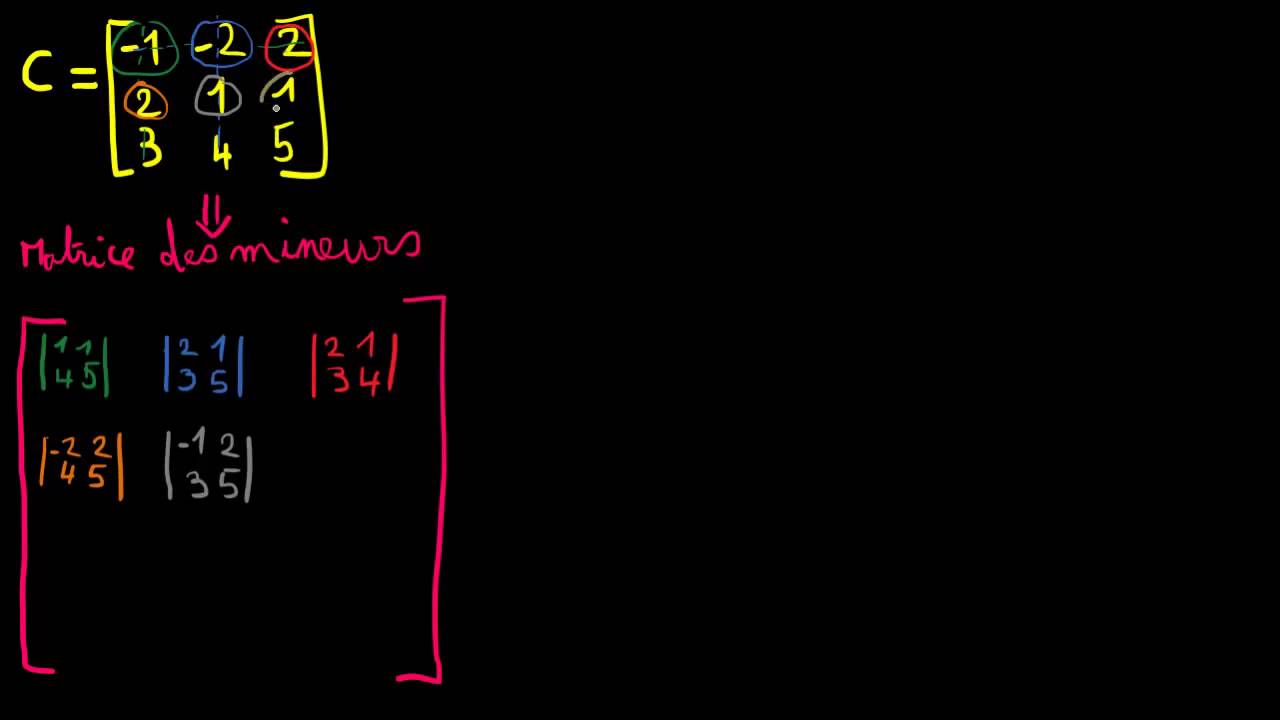Comatrice

En algèbre linéaire, la comatrice d'une matrice carrée A est une matrice carrée de même taille, dont les coefficients, appelés les cofacteurs de A, interviennent dans le développement du déterminant de A suivant une ligne ou une colonne. Si A est une matrice inversible, sa comatrice intervient également dans une expression de son inverse.

Dans cette page, A désigne une matrice carrée d'ordre n à coefficients dans un anneau commutatif K.

Définitions

Le cofacteur d'indice i, j de A est :

${\displaystyle \left(\operatorname {com} A\right)_{i,j}{\overset {\underset {\mathrm {def} }{}}{=}}\det \left(A'_{i,j}\right)=(-1)^{i j}\det \left(A_{i,j}\right)}$, où

• A'_i,j est la matrice carrée de taille n déduite de A en remplaçant la j-ème colonne par une colonne constituée uniquement de zéros, sauf un 1 sur la i-ème ligne ;
• A_i,j est la sous-matrice carrée de taille n – 1 déduite de A en supprimant la i-ème ligne et la j-ème colonne (son déterminant fait donc partie des mineurs de A).

La comatrice de A est la matrice de ses cofacteurs.

Formules de Laplace

On peut calculer le déterminant de A en fonction des coefficients d'une seule colonne et des cofacteurs correspondants. Cette formule, dite formule de Laplace, permet ainsi de ramener le calcul d'un déterminant d'ordre n à celui de n déterminants d'ordre n – 1.

Formules de développement d'un déterminant d'ordre n :

• par rapport à la colonne j :

  ${\displaystyle \det A=\sum _{i=1}^{n}a_{i;j}(\operatorname {com} A)_{i,j}}$ ;

• par rapport à la ligne i :

  ${\displaystyle \det A=\sum _{j=1}^{n}a_{i;j}(\operatorname {com} A)_{i,j}}$.

Généralisation

La formule suivante se déduit des formules de Laplace et les inclut :

${\displaystyle A\;{}^{\operatorname {t} }\!{\operatorname {com} A}=\left({}^{\operatorname {t} }\!{\operatorname {com} A}\right)\;A=\left(\det A\right)\;\mathrm {I} _{n}}$,

où I_n désigne la matrice identité de même taille n que A.

La matrice transposée de la comatrice est appelée matrice complémentaire de A. Notamment si det A est inversible dans K, alors A est inversible dans M_n(K) et son inverse est un multiple de la matrice complémentaire, ce qui veut dire qu'on a obtenu une formule pour l'inverse, ne nécessitant « que » des calculs de déterminants :

${\displaystyle A^{-1}={\frac {1}{\det A}}\,{}^{\operatorname {t} }\!{\operatorname {com} A}}$.

Cette formule n'a guère qu'un intérêt théorique car en pratique, elle est trop lourde pour calculer explicitement A⁻¹ dès que n ≥ 4 et la méthode plus élémentaire à base d'opérations élémentaires sur les lignes (inversion par pivot de Gauss) est plus efficace, aussi bien pour l'humain que pour la machine.

Propriétés de la comatrice

• Compatibilité avec la transposition : com(^tA) = ^t(com A).
• Compatibilité avec le produit : com I_n = I_n et pour toutes matrices carrées A et B d'ordre n, com(AB) = (com A)(com B).
• Rang (si K est un corps commutatif) :
  • si A est de rang n (c.-à-d. A inversible), com(A) aussi (jointe à la précédente, cette propriété assure que l'application « comatrice » se restreint en un automorphisme du groupe linéaire GL_n(K)) ;
  • si A est de rang n – 1, avec n ≥ 2, com(A) est de rang 1 ;
  • si A est de rang inférieur ou égal à n – 2, com(A) = 0.
• Déterminant : si n ≥ 2, det(com A) = (det A)^n–1.
• Comatrice de la comatrice : si n ≥ 2, com(com A) = (det A)^{n – 2} A.
• Si P(X) = det(A – X I_n) est le polynôme caractéristique de A et si Q est le polynôme défini par Q(X) = (P(0) – P(X))/X, alors : ^t(com A) = Q(A).

Exemples

Matrices de taille (1,1)

La comatrice de toute matrice de taille (1,1) est la matrice identité I₁ = (1).

Matrices de taille (2,2)

${\displaystyle \operatorname {com} {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{pmatrix}d&-c\\-b&a\end{pmatrix}}}$.

Matrices de taille (3,3)

${\displaystyle \operatorname {com} {\begin{pmatrix}a_{11}&a_{12}&&a_{13}\\a_{21}&a_{22}&&a_{23}\\a_{31}&a_{32}&&a_{33}\\\end{pmatrix}}={\begin{pmatrix} {\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}}&-{\begin{vmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\end{vmatrix}}& {\begin{vmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{vmatrix}}\\-{\begin{vmatrix}a_{12}&a_{13}\\a_{32}&a_{33}\end{vmatrix}}& {\begin{vmatrix}a_{11}&a_{13}\\a_{31}&a_{33}\end{vmatrix}}&-{\begin{vmatrix}a_{11}&a_{12}\\a_{31}&a_{32}\end{vmatrix}}\\ {\begin{vmatrix}a_{12}&a_{13}\\a_{22}&a_{23}\end{vmatrix}}&-{\begin{vmatrix}a_{11}&a_{13}\\a_{21}&a_{23}\end{vmatrix}}& {\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}}\end{pmatrix}}}$.

On rappelle que ${\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc}$ (voir déterminant).

Variations de la fonction déterminant

On suppose ici que K est le corps des réels, et l'on s'intéresse à l'application déterminant, vue comme fonction des coefficients de la matrice :

${\displaystyle \mathbb {R} ^{n^{2}}\simeq \mathrm {M} _{n}(\mathbb {R} )\to \mathbb {R} ,\;A\mapsto \det A}$.

La formule de Leibniz montre que c'est une fonction polynomiale (homogène) donc indéfiniment différentiable.

On peut retrouver et préciser cette régularité grâce aux formules de Laplace (voir supra) : en un point A quelconque de M_n(ℝ), la fonction det est affine par rapport à la variable d'indice i, j, et sa dérivée partielle est le cofacteur de A de même indice :

${\displaystyle {\frac {\partial \det }{\partial A_{i,j}}}(A)=(\operatorname {com} A)_{i,j}.}$

On en déduit, toujours au point A, le gradient de det (si l'on munit M_n(ℝ) de son produit scalaire canonique) : ${\displaystyle \nabla \det(A)=\operatorname {com} A}$

ou encore, sa différentielle donc son développement limité à l'ordre 1 : ${\displaystyle \det(A H)=\det A {\rm {tr}}\left(\left({}^{t}\!\operatorname {com} A\right)H\right) o\left(\left\|H\right\|\right)}$.

Notamment pour le cas où A est la matrice identité : ${\displaystyle \nabla \det(\mathrm {I} _{n})=\mathrm {I} _{n}{\text{ et }}\det(\mathrm {I} _{n} H)=1 {\rm {tr}}(H) o(\|H\|)}$.

Comatrice et produit vectoriel

Si A est une matrice réelle d'ordre 3, elle agit sur les vecteurs de l'espace euclidien orienté ℝ³. La comatrice de A décrit alors l'interaction de A avec le produit vectoriel :

${\displaystyle Au\wedge Av=\operatorname {com} A\,(u\wedge v)}$.

Notes et références

• Portail de l’algèbre