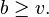Inégalité de Fisher

En mathématiques combinatoires, l'inégalité de Fisher est une condition nécessaire pour l'existence d'un plan en blocs incomplet équilibré, c'est-à-dire d'une famille de parties d'un ensemble qui remplissent certaines conditions prescrites. L'inégalité a été esquissée par Ronald Fisher, généticien et statisticien de la génétique des populations, qui s'intéressait aux plans d'expériences pour l'étude des différences entre plusieurs variétés de plantes dans des conditions de croissance différentes.

Énoncé

Soient

v le nombre de variétés de plantes;
b le nombre de blocs.

Dans un plan en blocs incomplet équilibré, trois paramètres interviennent :

k, le nombre de variétés différentes figurent dans chaque bloc, avec 1 ≤ k < v ; aucune variété ne doit apparaître deux fois dans un même bloc;
λ, le nombre de blocs où deux variétés quelconques apparaissent simultanément ;
r , le nombre de blocs contenant chaque variété.

L'inégalité de Fisher est simplement la formule :

Démonstration

Soit M la matrice de dimensions v × b définie par M_i,j = 1 si l'élément i est dans le bloc j et 0 sinon. La matrice B = MM^T (où M^T est la transposée de B ) est une matrice de dimensions v × v telle que B_i,i = r et B_i,j = λ pour i ≠ j . Puisque r ≠ λ, on a det(B) ≠ 0, donc rang(B) = v ; d'autre part, rang(B) ≤ rang(M) ≤ b, donc v ≤ b .

Généralisation

L'inégalité de Fisher est valable pour des classes de designs plus généraux : un plan en blocs équilibré par paire (ou PBD) est un ensemble X avec une famille de sous-ensembles non vides de X (pas nécessairement de même taille et pouvant contenir des répétitions) de sorte que chaque paire d'éléments distincts de X est contenue dans exactement λ > 0 sous-ensembles. L'ensemble X peut être lui-même l'un des sous-ensembles, et si tous les sous-ensembles sont des copies de X, le PBD est appelé "trivial". La taille de X est v et le nombre de sous-ensembles dans la famille (compté avec multiplicité) est b .

Ce résultat généralise également le théorème de De Bruijn-Erdős (géométrie d'incidence) :

Dans une autre direction, Ray-Chaudhuri et Wilson ont prouvé en 1975 que dans un plan de paramètres 2s-(v, k, λ), le nombre de blocs est au moins ${\binom {v}{s}}$ .

Notes

Références

Bose_(Raj_Chandra)1949'>Bose (Raj Chandra), « A Note on Fisher's Inequality for Balanced Incomplete Block Designs », Annals of Mathematical Statistics,‎ 1949, p. 619-620Bose (Raj Chandra)&rft.date=1949&rft.pages=619-620&rfr_id=info:sid/fr.wikipedia.org:Inégalité de Fisher">.
Fisher_(Ronald_Aylmer)1940'>Fisher (Ronald Aylmer), « An examination of the different possible solutions of a problem in incomplete blocks », Annals of Eugenics, vol. 10,‎ 1940, p. 52-75 (DOI 10.1111/j.1469-1809.1940.tb02237.x)Fisher (Ronald Aylmer)&rft.date=1940&rft.volume=10&rft.pages=52-75&rft_id=info:doi/10.1111/j.1469-1809.1940.tb02237.x&rfr_id=info:sid/fr.wikipedia.org:Inégalité de Fisher">
Stinson (Douglas R.), Combinatorial Designs: Constructions and Analysis, New York, Springer, 2003 (ISBN 0-387-95487-2)Stinson (Douglas R.)&rft.date=2003&rft.isbn=0-387-95487-2&rfr_id=info:sid/fr.wikipedia.org:Inégalité de Fisher">
Street_(Anne_P.)class="petites_capitales"_style="font-variant:_small-caps;">Street_(Deborah_J.)1987'>Street (Anne P.) et Street (Deborah J.), Combinatorics of Experimental Design, Oxford University Press, 1987, xiv 400 (ISBN 0-19-853256-3)Street (Anne P.)&rft.au=Street (Deborah J.)&rft.date=1987&rft.tpages=xiv + 400&rft.isbn=0-19-853256-3&rfr_id=info:sid/fr.wikipedia.org:Inégalité de Fisher">

Énoncé

Démonstration

Généralisation

Notes

Références

Articles liés